Author: Ludvík KoutnýLudvík is a 20 years old self-taught 3D artist based in Czech Republic, who has been interested in 3D for about 4 years now. He’s been working professionally in the architectural visualization field for the past 2 years in Michelle Bivotti visualization studio. Not having any official CG or Architecture related education, he gains all the knowledge that is directly tied to the Archviz profession in his spare time, thus actively educating himself and working at the same time.

Rendering

The rendering setup in MR is probably not as complex as some of you might think. There are several settings you need to focus on, to successfully setup and render your scene.

First, I will cover two most important ones…

Indirect illumination and Antialiasing

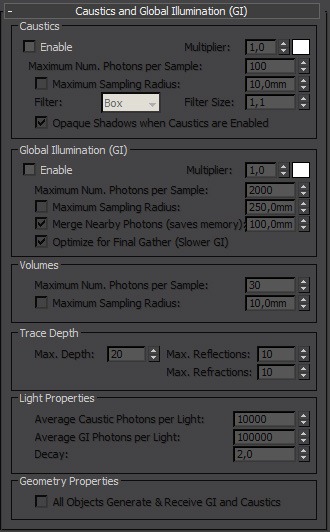
For indirect illumination, MR offers Global Illumination, which is basically a very stupid confusing term for photon mapping (GI from now on), and Final Gather (FG from now on).

The workflow is meant to work as follows…

GI first emits photons around the scene, saves photon map, and FG then calculates for fine indirect illumination while using data from GI to estimate secondary bouncing.

You can not use GI without FG if you want to get good results, but may use FG without GI. Every method has it’s drawback which I’m going to try to explain here.

Global illumination calculation is extremely fast, and provides also secondary bounces for FG, so it speeds up rendering quite a bit. Unfortunately, it is emitted from light sources, thus you always have to focus your photon flows in order for it to pre-calculate correctly. Photon emission is in general very inefficient, and it’s inefficiency grows even further in complex scenes.

You also cannot use photon mapping without portal lights to light everything, because photons are not emitted from the environment (sky). That means if you use FG + GI on some scene without portal lights, FG will only pick up first bounce from sky, because once GI is activated, any FG secondary bounces are disabled. Then any secondary bouncing comes only from sun, not from sky, and ratio of secondary bouncing is extremely incorrect (only yellow light contribution of sun, but no blue light contribution of sky).

Only real lights, those you can create and manipulate in viewport, can emit photons. Environment maps or luminous materials can not.

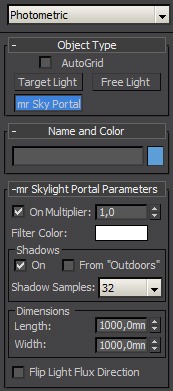
Portal Lights

Portal lights, are lights that basically take the environment color, and project it inside of an interior on area light basis. They do not add nor subtract intensity of environment, just pass it through on a directional light basis.

This has several benefits:

1. Superb shadow definition from environment lighting.
2. Emits photons (thus balances contribution of secondary light bouncing when GI is used).
3. Helps FG to get environmental illumination through openings into an interior.

Drawbacks are:

1. Directional area light sampling increases render time, especially when many light sources are present.
2. When used, only interior (area inside of openings covered by portals) has correct indirect illumination. So exterior has only 1st bounce from final gather, and photons from possible sunlight, but not skylight.
3. Does not pass FG rays through, so it is very problematic when looking from an exterior into interior through an opening covered by portal light.

Final Gather

FG is a bit similar to Irradiance cache. Rays get basically shot from camera into the scene, with some spacing that is defined by several importance parameters, such as geometry density, lighting contrast, etc… And then bounce around the scene to the light source, and deliver light back through the path they traveled, in order to indirectly illuminate all the surfaces. You can set an amount of indirect bounces, or use GI to handle secondary bouncing.

FG secondary bouncing is a lot slower, and produces high variance that can result in blotches and artifacts, but is all around a lot more universal solution, and works in many scenarios where GI tends to fail.

So now, when you know all of this, I can explain why I made the rendering decisions I made. Esherick House was quite a difficult scene to illuminate with MR’s indirect illumination toolset.

I could not use portal lights, because there is a lot of windows, those large ones are divided into smaller ones, and every one of them would require it’s own portal light, and that would make my render times extreme, as well as add significant amount of noise. Also on a lot of the shots, you could see the interior from the exterior, and since portals do not pass FG rays through, there would be some artifacts on the edges of window openings.

Then, portals would only pickup environment, but would ignore all the objects outside of the house, and provide me with incorrect illumination. Portal lights have an option to sample outdoor objects as well, but that is very slow, would be even slower considering the amount of objects (foliage) I had there, and add that to slowness due to the high portal light count…

I would see first final frame finished when I would be like 90 years old 😀

Definitely no portals. And that directly leads to impossibility of using GI because if there were no portals, then there would be no GI from sky environment, and my secondary light bouncing would get corrupted.

So, the only option left is…  FG alone with multiple indirect bounces.

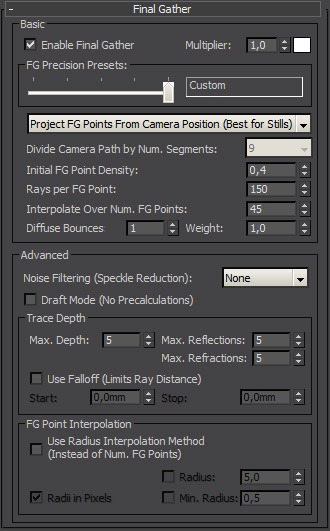
Now, let’s break down important FG settings. There is not many of them, and they are very easy to understand 🙂

1. Initial FG Point Density is basically a density of samples. Amount of samples that will be shot from camera.
2. Rays per FG Point is quality of those samples. How many rays will be shot from every samples to estimate illumination of the surrounding environment, and use it to illuminate sampled area.
3. Interpolate Over Num. of FG Points is simply amount of interpolation. It is a tradeoff. Higher value will make your indirect illumination smoother, with less blotchiness, but will reduce the shadow detail of indirect illumination. Lower value will increase variance (blotchiness) but also increase accuracy and thus retain more detail.
4. Diffuse bounces is general amount of indirect bounces.
5. Weight value is multiplier of FG intensity. You should never, ever… EVER, change this value!
6. Noise filtering is a filter that is supposed to reduce amount of blotches, by ignoring rays, that carry light information, that is in significant contrast with average of all other values collected by other rays. This might sometimes be useful, but in general, it introduces significant bias, and it’s basic principal is really lame and not very beneficial. So I suggest you always set it to none.
7. Trace depth defines how deeply will be traced reflective and refractive components of shaders. Max. Depth value should be sum of Max. Reflection and Max. Refraction. values. For final gather, you should get by with using depth of 2 Reflection, 2 Refraction. and 4 total.
8. Radius interpolation is legacy interpolation method. While it retains detail significantly better than point interpolation, it does not know how to interpolate samples in reflections, which renders it pretty much useless. So I advise against using it.

Esherick House Render Settings

Now, finally for the settings. For the Interiors I have used:

• 0,5 point density
• 1000 rays
• 80 interpolation points
• 4 diffuse bounces

I had to use pretty high ray amount to make sure enough rays get from the interior all the way to the skylight, and bring back enough illumination.

For exteriors, you can get away with significantly lower settings, in my case:

• 0,5 point density
• 200 rays
• 30 interpolation points
• 2 diffuse bounces

When you use conventional method of FG + GI, then simply use the presets that are there. Low is usually good for previews, medium for final rendering, draft for drafts. Do not forget to set filter to none, and if you encounter blotches, just leave preset as it is, and increase point interpolation value until they go away.

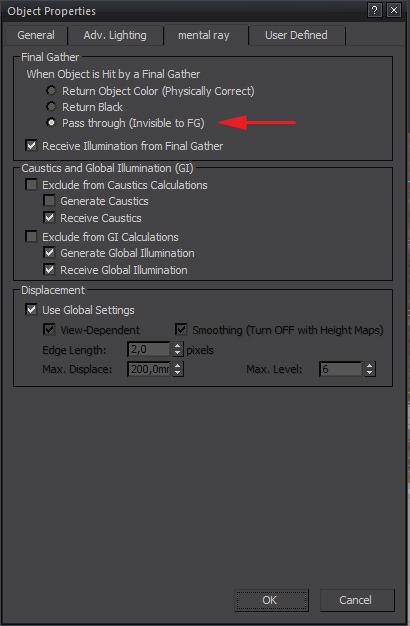
Also, in order to reduce amount of data FG needs to calculate, and thus speed up my rendering, I have excluded glass covering windows from FG sampling.

Make sure you leave “Receive illumination from FG” turned on. Only switch tick box to Pass through.

It is also good to disable shadow casting of glass planes, so directional lights have easier work. This applies only for glass planes in windows. For all other glass object in your scene, leave shadows enabled! Also, leave “Receive shadows” enabled.

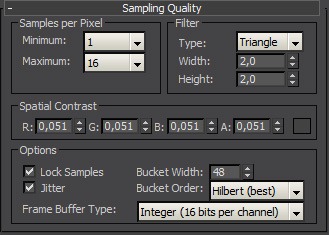
Antialiasing is pretty straightforward and very easy, you have several settings at your disposal:

Min. and Max. defines minimum and maximum amount of AA samples.

• Spatial contrast is a color threshold, that defines where Min and where Max amount of samples is used. Lower setting generally increases quality, but render time as well. You will not need to change this value very often. So if you do not know what you are doing, just leave it as it is, at 0.051
• Lock samples is a feature, that helps maintaining sampling integrity in animation. (That’s how I understand it, I did not really dig deep into it, I just leave it turned on)
• Jitter is a function, that offsets AA sampling rays in random direction, to increase chances of picking up thin lines, that are parallel to horizontal or vertical edge of a picture. If the sampling was not jittered, then some very thin lines could slip between sampling pattern, and would not be picked up at all. So leave this function turned on.

Filters are just filters…  What can I say, I just cannot think of any definition right now. They are basically different curves used to blend between pixels when they are antialiased. I already feel like I am writing a book here, so I will not explain every one of them. Just a simple advice:

Use Triangle at Width = 2 & Height = 2 for previews, and Mithchell at Width = 4 & Height = 4 for finals. 🙂

Now for the settings themselves:

• Use Min 1/16 – Max 1 for fast drafts.
• Use Min ¼ – Max 4 for mid-quality previews.
• Use Min 1 – Max 16 for final renderings.
• Use Min 4 – Max 64 for some extremely fine renders. This is usually good for shots of objects, where you need superfine detail, such as studio shots of cars.

It is as simple as this 🙂

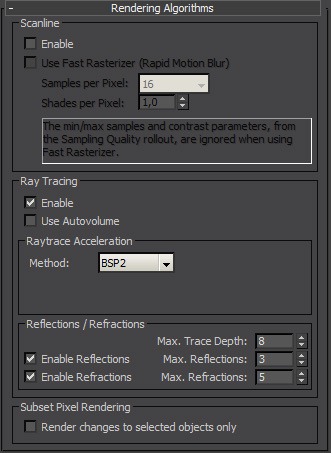
Next tab that was important in setting up Esherick House scene was Rendering Algorithms tab. I will not dig through every setting, I will just explain why I have set it this way.

I have disabled Scanline. It might by enabled by default. Anytime you are about to create any complex scene, pretty much anything that has 1,000,000 polys, always disable it. It will allow MR to work with memory more dynamically.

Ray trace acceleration

Always use BSP2, it is a new ray trace acceleration method, very memory efficient, fast in complex scenes, and fully automatic, just use it, simple as that 😉

Reflections and refractions settings are self-explanatory. It simply sets amount of ray tracing depth for reflections and refractions. Same as in FG applies – Total trace depth should be always sum of reflection + refraction depth. The settings you can see on the picture usually work for me very well in 99% of the cases, so i do not change them 🙂

Do not worry if your refraction depth is not large enough, you will not get black refraction. After a ray runs out of refraction depth, it just ignores any transparent objects, and returns color of a first opaque object it hits, or in case there is no object, it returns environment color. This smart mechanism is introduced in MR 3.7.

That is pretty much all about rendering. I know I did not cover a lot of the remaining settings, but I already wrote more than enough, and I did not cover them because I did not use them / their setup did not differ from defaults.

I did not cover standard interior lighting approach as well as GI settings, so I am attaching a classroom scene (shared above), originally made and kindly shared by Alex Sandri, shaded and lit in MR, so you can use it as a reference of standard interior lighting setup. You need at least 3ds Max 2012 to open it.

Post Production

I will try to describe my usual Photoshop post processing process. First of all, I always flatten image, always, after every step I do. I know that I lose a lot by not keeping layers, and that I cannot go in previous layer and make some adjustments, but I feel like flattening image after every step gives me a lot more freedom. This is my way, and might not fit all.

Starting with raw render…

Usually, when I open any rendered image, its little dark and strongly washed out. First step is to brighten the image up using brightness/contrast function. I usually add about +20 to +40 brightness points, depends on how dark the initial image is.

Next step is to add some contrast. I duplicate the image into a new layer, set mode to soft light, and set layer opacity to about 25%. Then I blur the image using Gaussian blur with some large radius, let’s say 25 pixels. This will give the image some slight contrasty glow.

As a next step, I repeat the same process, but without blurring, and I set the layer opacity to about 10-30% to make it even slightly more contrasty.

Next, I duplicate the layer again, and I use auto color function. This turns most of my images into bluish cold tones, I then set the mode of layer to color. That will transfer cold bluish color tones on the bottom layer, but without transferring additional contrast to it.

Once I got slightly washed out cold-toned image, I duplicate layer once again, put rich 100% yellow color in my primary swatch, and rich 100% red in my secondary swatch, and then apply gradient map function on my duplicated layer. After that, I set layer to soft light mode with about 20% opacity. This will combine cold tones with some warm tones, and give you pretty nice color mood.

After that, I select all the bright sky overexposed areas with magic wand tool, that has tolerance of about 25, create a new layer, fill selection with blue sky color, deselect, apply Gaussian blur with about 50-100pix radius, and then set layer mode to screen. That makes those nice blue glow effect around the windows, and around the sky on some exteriors.

I repeat the similar process on very bright sun streak areas, with some slight differences. I use smaller blur radius here (10-50px) orange color, and sometimes I use color dodge mode instead of screen mode.

In next step I use lens correction filter to add some subtle vignette effect and sometimes also to add slight chromatic aberration effect. But be careful with CA, it tends to blur your image a bit.

Then I usually sharpen my image using unsharp mask filter, set to 50% with 0.5px radius and 0 threshold.

After that, I use color balance tool to fine tune my color tones. I often put 5, 0, -5 in shadows, and -5, 0, 5 in highlights. I have Preserve luminosity always active.

Last step is to add noise, for that i simply use add noise filter set to monochromatic Gaussian at 1%.

Then I just once more fine-tune brightness using brightness/contrast function.

I sometimes also experiment with Nix Color Efex filter set for PS i got with my Wacom tablet. It is really great set of filters with some neat features to control them. I recommend you give it a try 🙂

The final image…

Summary

I think that’s all folks 🙂

This was a long stretch and I’m sure I forgot some things I wanted to cover in this 4 parts series, but I still hope there won’t be some significant missing pieces of the puzzle. I am also sorry for possible grammar mistakes. My English is not that bad, but I could not pay attention to it while writing this article, since my head was full of Esherick House and Mental Ray 😀 (Luckily, Ronen is going to do some editing, so I won’t be as much embarrassed as if I published it on my own 😀 )  And of course, my fingers were a lot slower than my mind, so I was writing it down in a rush 🙂

If you have any questions, just publish them down in the comment box, and I will do my best to try to answer them 🙂

I hope that these articles helps you mainly when you decide to give MR a shot. And if you already are a MR user, then you might find there some tricks to incorporate in your own workflow 🙂